tutorials :: Kreisdiagramme

Inhalt
Worauf zu achten ist Die Konstruktion Ein Kreissektor Die Beschriftung Alle Kreissektoren Zusammenfassung

Kreisdiagramme sind ein denkbar schlechter Weg Informationen über ein Merkmal darzustellen. Für Menschen ist es nämlich schwieriger, Flächen als Längen miteinander zu vergleichen. Das wird zum Einen von Psychologen behauptet und zum Anderen von empirischen Untersuchungen gestützt. Vor Allem bei relativ vielen Merkmalsausprägungen wird der Vergleich von Kreissektoren schwierig. Wann immer es geht, sollte man deshalb auf Kreisdiagramme verzichten und stattdessen z.B. Säulen- oder Balkendiagramme benutzen.

Worauf zu achten ist

Hat man sich trotz obiger Bedenken für ein Kreisdiagramm entschieden, so gibt es noch eine Reihe von Dingen, die zu beachten sind. In erster Linie ist dabei eine ausreichende Beschriftung zu nennen. Zu jedem Kreissektor gehört nicht nur der Anteil der Merkmalsausprägung am Ganzen in Form der Prozente, sondern auch die entsprechende Fallzahl. Außerdem sollte man grafische Spielerein wie z.B. 3D-Effekte unterlassen, da sie die Darstellung verzerren.

Die Konstruktion

Als Beispiel betrachten wir die m²-Verteilung innerhalb der statistiker-wg, die wie folgt gegeben ist (gesamt: 94m²):

Bewohner	Fläche in m²	rel. Hfgkt.
Jule	12	0.128
Janna	10	0.106
Marcus	9	0.096
Paul	8	0.085
gemeinsam	55	0.585

Ein Kreissektor

Grundlage für den ersten Kreissektor ist eine horizontale Linie die gerade so lang wie der Radius des Kreisdiagrammes ist. Ich habe mich für einen Radius von 3cm entschieden. Der Winkel 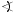eines jeden Kreissektors wird durch die relative Häufigkeit der jeweiligen Merkmalsausprägung bestimmt, und zwar durch die Formel

Für den Kreissektor von Jule erhalten wir somit einen Winkel von 46.08°. Hierbei gibt es schon das erste Problem. Der path-Befehl, mit dem wir den Kreissektor konstruieren, erlaubt nur ganzzahlige Angaben von Winkelgrößen, d.h. wir müssen die Winkel runden. Das Problem soll uns hier aber erstmal nicht weiter beschäftigen.

Dem path-Befehl übergibt man den Start- und Endwinkel sowie den Radius des Sektors. Die Winkelaufteilung in TikZ entspricht dabei folgender Grafik:

back to top

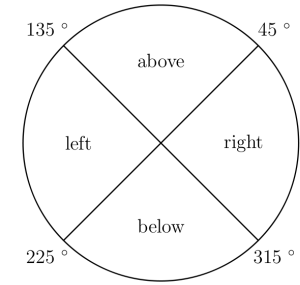
Fangen wir also bei 0° an, so wird das erste Kreisstück von ganz rechts nach links oben gezeichnet. Die verwendete Syntax ist nun denkbar einfach. Zuerst wird mit draw eine gerade Linie mit einer Länge von 3 cm gezeichnet. Während das erste Koordiantenpaar - der Startpunkt (0,0) - standardmäßig in cm angegeben wird, benutzt man beim zweiten bereits die Winkelangabe und die Länge des Radius, nämlich (0:3cm). Das bedeutet nichts anderes, als dass der zweite Punkt um drei Zentimeter vom Ursprung entfernt ist und dabei um 0° verschoben ist. Direkt hinter dem zweiten Koordinatenpaar kommt der arc-Befehl zum Einsatz. Er zeichnet vom Punkt (0:3cm) mit der Angabe von (0:46:3cm) eine Kreislinie von 0° bis 46°, wobei der Abstand vom Punkt (0,0) genau 3 cm beträgt.

\definecolor{myblue}{HTML}{92dcec}
\begin{tikzpicture}

  \draw[fill=myblue, thick] (0,0) -- (0:3cm) arc (0:46:3cm);

\end{tikzpicture}
    

back to top

Der linke äußere Strich fehlt, da genau an dieser Stelle der nächste Teil des Kreises ansetzen wird.

Die Beschriftung

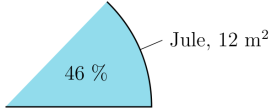
Auch bei einem Kreisdiagramm muss eine ausreichende Beschriftung vorhanden sein. Dazu zählt vor Allem der Name der Merkmalsausprägung, die relative Häufigkeit in Form der Prozente und die absolute Häufigkeit, hier also die Anzal m². Ich habe mich entschieden, die Prozente innerhalb des Kreissektors und Jules Namen sowie die m²-Anzahl außerhalb zu schreiben. Das Ergebnis sieht dann so aus:

  \draw[fill=myblue, thick] (0,0) -- (0:3cm) arc (0:46:3cm)
      node at (23:1.8cm) {46 \%};
  \draw (23:3cm) -- (23:3.5cm) node[right] {Jule, 12 m$^2$};
    

back to top

Zuerst wird mit dem node-Operator in der Mitte die Prozentzahl geschrieben. Dazu brauche ich den Winkel der zwischen 0° und 46° liegt, also 23°. Ein geeigneter Abstand zum Mittlepunkt stellt 1.8 cm dar. Vom Kreisrand aus wird mit dem draw-Befehl ein dünner, 0.5 cm langer Strich bei ebenfalls 23° gezogen, an dessen Ende mit Hilfe von node der Name der Merkmalsausprägung und die zugehörige Quadratmeteranzahl hinzugefügt wird. Dabei wird der Name rechts vom Ende des Striches geschrieben. Das sieht dann gut aus, wenn der Winkel, an dem der Strich gezeichnet wird, zwischen 315° und 45° liegt. Was bei welchem Winkel anstatt von right stehen sollte, kann man der folgenden Grafik entnehmen:

back to top

Alle Kreissektoren

Das, was wir oben für einen Kreissektor gemacht haben, müssen wir nun für alle Kreissektoren machen, d.h. wir müssen den Winkel berechnen, die Mitte des Kreissektors finden und ihn ausreichend beschriften.

Wir können nun entweder die restlichen Teilstücke einzeln schreiben, oder wir benutzen die foreach-Schleife. Obwohl wir hier eine überschaubare Anzahl von Merkmalsausprägungen vorliegen haben, entscheide ich mich für die foreach-Schleife. Dafür brauchen wir sechs Variablen: den Start- (start), End- (end) und Mittelwinkel (middle), die Prozentzahlen (percent), die äußere Beschriftung (outer) sowie deren Ausrichtung (anchor). Um das jetzt nicht alles selbst ausrechnen zu müssen, habe ich eine einfache (und nicht gerade gut programmierte) Funktion mit dem Namen latex.pie in R geschrieben, die das für einen beliebigen Vektor übernimmt. Das Ergebnis könnt ihr in der Zusammenfassung betrachten.

Zusammenfassung

Auch dieses tutorial soll keine Anleitung zur Konstruktion von Kreisdiagrammen liefern. Zum Einen ist TikZ nur in der Lage ganzzahlige Winkelgrößen zu verarbeiten, weshalb eine exakte Darstellung der Kreissektoren auf grund von Rundungen nicht möglich ist. Zum Anderen gibt es bessere Darstellungsformen, wie bereits erwähnt. Trotzdem hoffe ich, dass dieses tutorial den einen oder anderen hilfreichen Quellcode beinhaltet. Hier dann das Ergebnis.

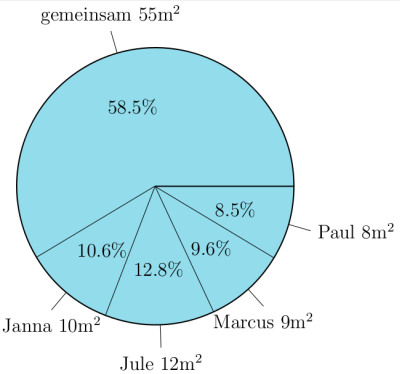
\definecolor{myblue}{HTML}{92dcec}
\begin{tikzpicture}

    \foreach \start/\end/\middle/\percent/\anchor/\name/\smeter in {
      0/211/106/58.5/above/gemeinsam/55,
      211/249/230/10.6/below/Janna/10,
      249/295/272/12.8/below/Jule/12,
      295/329/312/9.6/below/Marcus/9,
      329/360/344/8.5/right/Paul/8}
  {
    \draw[fill=myblue, thick] (0,0) -- (\end:3cm) arc (\end:\start:3cm)
      node at (\middle:1.8cm) {\percent \%};
    \draw (\middle:3cm) -- (\middle:3.5cm) node[\anchor] {\name \ \smeter m$^2$};
  };

\end{tikzpicture}
    

back to top